I. Introduction
     An alternative to the photovoltaic cell is the photoelectrochemical (PEC) cell. This cell utilizes an n- or p-type semiconductor as one electrode and platinum or carbon as the counter electrode, and these are connected through an external circuit. The semiconductor-electrolyte interface is similar to a Schottky junction. A space-charge layer develops in the semiconductor such that band-gap radiation falling on the semiconductor will effectively separate the electrons and holes at the interface. This provides the photovoltage to generate a current in the external circuit.

     It should be understood that a PEC cell can serve several functions. If the electrolyte contains only one redox couple, no net chemical change occurs in the cell, and the net effect is the generation of electric current. In this case the PEC cell is called a photovoltaic electrochemical cell. If two redox couples are present, a net chemical reaction can take place. Sometimes a distinction is made depending on the sign of the free energy change. If ΔG > 0, the PEC cell is said to be a photoelectrosynthetic cell. If ΔG < 0, the cell is called a photocatalytic cell. This latter cell was first used by Fujishima and Honda in 1972 to split the water molecule into hydrogen and oxygen. They used n-type TiO₂ and platinum electrodes in a biased cell. The need for an anodic bias resulted in a photoassisted electrolysis cell. The term "PEC cell" usually stands for such a cell, whether biased or not.

     PEC cells have several advantages over photovoltaic cell. Thus, the semiconductor electrode can be made of polycrystalline material and the purity requirements are not as severe as in the case of single-crystal silicon photocells. The semiconductor-electrolyte interface is easy to make and is very effective in separating electrons and holes. The cell is versatile, being able to be run in either the photovoltaic or electrosynthetic modes. However, as a practical matter, the commercial application of PEC cells is fraught with difficulties. Just the construction of arrays of cells with large area electrodes is a formidable problem.

     If the Fermi level of a PEC cell employing an n-type photoanode lies below (i.e., more negative of) the redox potential of the species to be reduced, no external bias need be applied, and the cell will operate under short-circuited conditions. A similar statement holds for a p-type photocathode. This has very important implications for the construction of practical cells. It means that single-crystal or polycrystalline-wafer electrodes can be dispensed with. All that is necessary is a powder of the semiconductor, onto which is deposited a metal by photoreduction. These are called particulate systems or photochemical diodes and are very attractive from the standpoint of engineering problems and cost effectiveness. Furthermore, the concept of the p-n PEC cell, wherein an n-type anode is connected to ap-type cathode by an ohmic contact, can also be extended to particulate systems, although no one has yet solved the problem of making ohmic contacts between powders. Note: this may now be solvable with nanotechnology.

     The construction of photochemical diode devices was first explored in the period 1979-1981. Most of the work focused on the splitting of water, but other reactions were studied such as the oxidation of carbon, the photo-Kolbe reaction, and the oxidation of halogens. Although ingeneous particulate systems have been devised for the decomposition of water, no efficient and economical system has yet been found. In general, the funding for this type of research has been rather meager, probably because of exceptionally cheap oil and the generally-held view that solar energy will never be able to provide more than a small percentage of our energy needs. This type of research is really in the province of heterogeneous catalysis. Consequently, we shall call such solar cells heterogeneous photocatalysis (HPC) cells whether ΔG is positive or negative. Next we consider the theory of such cells.

II. The Theory of Schottky Junction Cells
     The theory of HPC cells is based on theories of the semiconductor-electrolyte interface. In Figure 1 is shown the usual energy-level diagram for a Schottky-type semiconductor-electrolyte interface. Figure 1a represents the energy levels in the semiconductor (SC), electrolyte, and metal before contact. Here E_c is the energy of the conduction band, E_v is the energy of the valence band, E_F is the Fermi energy (chemical potential of electrons) of the semiconductor,ε_F is the Fermi energy of the metal, and Φ_el is the Fermi energy of the redox couples in the electrolyte and is determined by the Nernst equation. The position of E_F in Fig. 1a is also called the flat-band potential, V_fb. It is desired to drive a reaction of the type

The energy levels in the semiconductor are usually expressed in electron volts (eV), while those in the electrolyte are in volts versus either the normal hydrogen electrode (NHE) or the saturated calomel electrode (SCE). The eV scale is referred to vacuum, while the volt scale is referred to the NHE, so that the relation between the two scales is

Thus, the zero on the volts scale is at -4.5 eV.

     Figure 1b shows the situation upon contact and after equilibrium has been attained in the dark. The Fermi levels must be equal at equilibrium and must equal φ_el. The electric potential set up across the semiconductor-electrolyte interface upon equilibration of the Fermi energies causes band bending by an amount V_B with respect to the surface. It is this band bending that provides the potential to separate electrons and holes at the surface.

     Upon illumination of the semiconductor-electrolyte surface with radiation of energy equal to or greater than the band-gap energy E_g = E_c - E_v, shown in Fig. 1c, the Fermi level moves toward V_fb. If V_fb and E_v bracket the two redox potentials, as shown, it is possible under illumination for the holes to oxidize B_red at the SC surface and for electrons to reduce A_ox at the metal surface:

     These energy relationships are also assumed to hold for HPC cells, although results of studies done on single-crystal or polycrystalline semiconductor wafers in PEC cells may not be exactly transferable to HPC cells, where the semiconductors may be composed of very small powder particles or even colloidal particles. Also, the actual situation is more complicated than indicated in Fig. 1, since surface states (dangling bonds, impurities, adsorbents, etc.) can cause large effects such as Fermi level pinning, which invalidates some of the above discussion when it occurs.

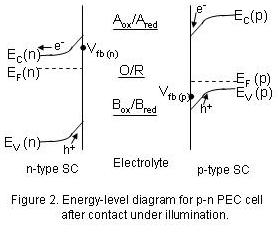
     The situation for p-n cells is shown in Figure 2, which is equivalent to the situation shown in Fig. 1c. This type of cell allows the use of small band-gap semiconductors, since the reduction of A_ox and oxidation of B_red are no longer dependent of V_fb (n) and V_fb (p), respectively. Such a cell was first constructed by Nozik [Appl. Phys. Lett. 29, 150 (1976)] utilizing n-type TiO₂ and p-type GaP to decompose water. Following the work of Bard at U. Texas, the general case can be schematically written as

Where D+/D, O/R, and C/C- are redox systems that act as relays between semiconductor particles or semiconductor and catalyst particles (CAT_O and CAT_R). The semiconductors can also be both n-type or both p-type and can have a sensitizer adsorbed on them. The redox couple O/R can be simply an ohmic contact. There are many variations of this scheme possible. Thus, for example, the particulate system

Has proven to be very efficient at water decomposition using ultraviolet radiation. The catalyst Pt/TiO₂/RuO₂ is composed of colloidal TiO₂ loaded with small amount of Pt and RuO₂. The Pt reduces the hydrogen overvoltage, and the RuO₂ is an extremely good hole scavenger, although its exact function is unknown. The H₂ yields can often be improved by adding sensitizers such as Ru(bipy)₃²⁺ and relays such as methylviologen (MV²⁺).

     The actual behavior of any HPC cell is dependent on many factors. These factors include:

1. Nature of couples
2. Nature of solvent
3. Nature of SCs
4. Pretreatment of SCs
5. Concentration of SCs
6. Size of SC particles
7. Amount of CAT_O and CAT_R loading
8. pH
9. Intensity of radiation
10. Wavelength of radiation
11. Temperature
12. Pressure
13. Sensitizers
14. Relays
15. Dopant impurities

In the next section, we consider the basic question, can HPC cells realistically be expected to solve the energy problem?

III. The Practicality of HPC Cells
     For sake of argument we consider only hydrogen production by the splitting of water. To be practical, a reasonable amount of hydrogen must be produced per square meter of solar cell area. To be economically feasible, the cost should be competitive with existing power-generating plants. These two points will be considered in turn.

     Treating the sun as a black body at 5900 K, a simple calculation shows that about 7 x 10²¹ photons per square meter per second strike the earth. If each photon were effective at water decomposition, it would be possible to produce hydrogen at the rate of 20.5 mol m^-2 h^-1. This rate is 460 liters at STP with an energy equivalent of about 5900 kJ. We assume an average energy consumption of 17,000 kJ h^-1 for a typical home. Thus, with 100% efficiency and utilizing all the solar radiation, the typical home would need a solar collector of 9 m² for 8 hours of maximum solar radiation. However, actual systems are not 100% efficient, and less than the maximum anount of black-body radiation reaches the surface of the earth.

     To be more realistic, we assume a semiconductor with a band gap of 2 eV and again assume that the sun is a black body. The actual amount of radiation reaching the earth?s surface is 4 to 5 x 10²¹ photons m^-2 s^-1. The difference between this value and the black-body value of 7 x 10²¹ photons m^-2 s^-1 can be incorporated into the efficiency of the solar cell. For black-body radiation and a 2 eV band gap, the effective photon flux is 2.2 x 10²¹ photons m^-2 s^-1. We define the efficiency as being the number of moles of hydrogen produced per mole of photons of energy ≥ E_g incident on the solar cell. The number of moles of hydrogen produced for a given band gap will be dependent on the atmospheric conditions, the reflection and absorption characteristics of the cell, and the characteristics of the semiconductor-electrolyte system. The latter includes electron-hole recombination rate, back reaction of products, as well as the factors mentioned in the previous section. Table I shows the size of the solar collector necessary for a typical home having an energy consumption of 17,000 kJ h^-1. For maximum efficiency (100%), a collector of 28 m² would provide the entire energy needs of the home. On the other hand, an efficiency of 0.01 (2%) would require 1390 m². A typical home could easily accommodate a rooftop collector of 28 m² and perhaps as much as 100 m². Therefore, to be 100% energy independent, a solar cell of at least 20-25% efficiency would be necessary. This efficiency would certainly be an upper limit for any HPC cell. Realistically, it may not be possible to get better than 5% efficiency. However, even at 5% efficiency, a 100 m² solar collector would provide nearly 20% of the 17,000 kJ h^-1, not counting the side benefit of solar heating. In an underdeveloped country, this rate might provide all the present energy needs of the country.